To answer to this question, we need to start from the physic concept of Angular Momentum.
Conservation of Angular Momentum
Considering 2 body, the angular momentum of body ![]() relative to
relative to ![]() is:
is:
(1) ![]()
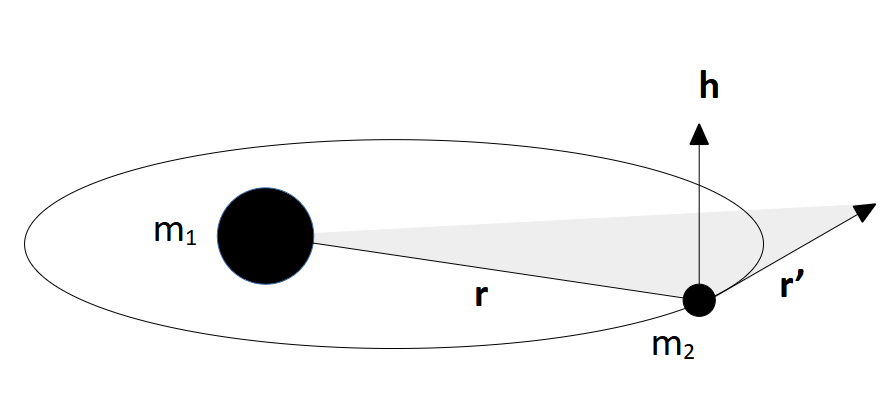
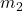 around
around 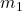 lies in a plane
lies in a planewhere ![]() . Dividing for
. Dividing for ![]() , it is defined the specific angular momentum.
, it is defined the specific angular momentum.
(2) ![]()
Now, we can find the derivative of ![]() :
:
(3) 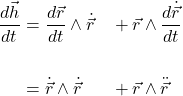
The first term is ![]() , since
, since ![]() .
.
Second term can be analyzed in this way:
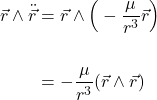
Since ![]() , also the second term is zero.
, also the second term is zero.
Therefore, angular momentum is conserved:
(4) ![]()
Conclusion
If the position vector and the velocity vector are parallel, then it follows from eq. (2) that the angular momentum is zero, and according to eq. (4), it remains zero at all points of the trajectory (rectilinear motion).
Considering a curvilinear trajectory, it is possible to state that the position vector and the velocity vector lie in the same plane (as illustrated in Figure 1). This means that the path of ![]() around
around ![]() lies in a single plane.
lies in a single plane.
Since ![]() , which explains why planets are forced to rotate around Sun. If there is a reduction in the position vector, there should be an increase in speed, in order to maintain the specific angular momentum constant.
, which explains why planets are forced to rotate around Sun. If there is a reduction in the position vector, there should be an increase in speed, in order to maintain the specific angular momentum constant.


Pingback: How Do Satellites Stay in Orbit? A Beginner's Guide - TheEngineeringHub
Pingback: Understanding Geostationary Orbit Equation and Radius