How Do Satellites Stay in Orbit? A Quick and Easy Guide

Introduction to Orbits

Have you ever wondered why satellites don’t just fall back to Earth? Or why they don’t drift away into space? Understanding how satellites stay in orbit is key to grasping the basics of space mechanics — and you do not need a PhD to follow along!

In this beginner-friendly guide, we’ll cover how satellites stay in orbit step by step, with simple explanations and just a touch of math.

Gravity: The Invisible Force That Keeps Us All Grounded

Let’s start from the basics, gravity is the force of attraction between any two masses. It pulls objects with mass toward each other. To make a simple example, on Earth, gravity is what keeps us grounded and causes objects to fall when dropped.

There are 2 main theories for the definition of gravity:

• The one discovered by Einstein, the general relativity that we are not going to cover in this article;
• The one discovered by Sir Isaac Newton that is totally valid for classic mechanics, that we are going to cover briefly in this section.​​

In the theory formulated by Newton it is possible to describe the gravity behavior in the following way:

Where:

• F is the gravitational force between two masses (in newtons, N)
• G is the gravitational constant:
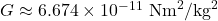
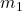• ​ and ​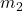 are the masses of the two objects (in kg)
• r is the distance between the centers of the two masses (in meters)

Not so easy to understand? Ok, let’s focus on the key concept of this formula. Newton, with this equation, wants to highlight that the gravity is a force that exists due to fact that mass exists. In particular, an object that has its own mass is able to attract another object, that provides another mass and vice-versa.

Therefore, Newton is saying that the force generated by the attraction of this two object is generated by the product of the 2 masses and G, the gravitational constant (that will not be investigated in this article, but you can find more details on TheEngineeringHub Blog). In addition, the distance (expressed with r) on the equation denominator means that this force is smaller, the smaller the distance is.

At a deeper level, gravity is one of the four fundamental forces of nature (along with electromagnetism, the strong nuclear force, and the weak nuclear force). Another thing that differentiate the gravity to other forces—like electromagnetism—is the fact that, since the mass has no positive or negative the gravity force is only positive, therefore is only an attractive force, unlike the electromagnetic one.

To come back on the original target, the main force keeping a satellite in orbit is gravity. Earth’s gravity pulls the satellite toward it, just like it pulls you and me toward the ground. But if that were the only force at play, the satellite would simply fall. So, what keeps it orbit and what allow to avoid crushing?

The Perfect Balance between speed and gravity

Imagine throwing a ball sideways. The faster you throw, the farther it travels before hitting the ground. Now, imagine throwing it so fast that as it falls, Earth’s surface curves away beneath it. That’s what a satellite does: it moves forward fast enough that keeps “falling around” Earth, never hitting the ground.

This balance between gravity and speed is what creates orbit.

Centripetal Force

For those curious about the math, the situation can be described with an equation. We only need to introduce the concept of centripetal force.

The centripetal force essentially is the force that keeps an object moving in a circular path and always acts toward the center of the circle. When something moves in a circle (like a satellite around Earth, a car around a curve, or a ball on a string), it means that the object is constantly changing direction — even if its speed stays constant. Changing direction means acceleration, and acceleration requires a force. That force is the centripetal force and can be described in the following way for an object of mass m moving at speed v in a circle of radius r:​

Where:

• r is the radius of the circular path (expressed in meters)
• F_c​ is the centripetal force (expressed in newtons, N)
• m is the mass of the object (in kg)
• v is the speed of the object (in m/s)

Simple Equation

The combination between the above mentioned centripetal force and gravity force will generate the simple equation described below. For simplicity, we are assuming that the satellite is performing a circular path.

Note: in the equation we are considering the two forces equivalent. This means that neither of them is able to counteract the other, and the motion of the satellite (or the object) will continue undisturbed. Therefore:

Where:

• m = mass of the satellite
• v = orbital speed
• r = distance from Earth’s center
• G = gravitational constant
• M = mass of Earth

Solving for v gives the orbital speed needed at a given altitude:

[Example] A low Earth orbit (LEO) satellite about 300 km above Earth needs to travel roughly 7.8 km/s (~28,000 km/h) to stay in orbit.

So the satellite needs to move at about 7.7 km/s (27,720 km/h) to stay in orbit at 300 km altitude.

Types of Orbits

There are several types of orbits that satellites can performs, in future article we will check the general theory and we will discover which are the most useful orbits. To provide some basic information, relevant to the circular ones, it is possible to identify the following:

Low Earth Orbit (LEO): 160–2,000 km altitude. Commonly used for Earth observation, environmental monitoring, and imaging satellites due to the close proximity to Earth. Also supports low-latency communication systems like satellite internet constellations (e.g., Starlink). To provide a significant example, the International Space Station (ISS) orbits at a mean altitude of approx 400km.

Geostationary Orbit (GEO): 35,786 km altitude. The satellite orbits at the same rate as Earth’s rotation, staying fixed over a single point on the equator. Ideal for continuous coverage — used in TV broadcasting, weather satellites, and long-range communications.

Polar Orbit: A special type of near-circular low Earth orbit that passes over Earth’s poles. As Earth rotates beneath it, the satellite eventually covers the entire surface. Widely used for global mapping, climate studies, reconnaissance, and Earth science missions.

Each orbit serves a unique role, chosen based on mission needs like coverage area, revisit frequency, resolution, and communication latency. Anyway, these are advanced topics that we are going to discover in the future.

What Happens Without Enough Speed?

Satellites rely on a delicate balance between gravity and orbital velocity to stay in space. If that balance is lost — specifically if a satellite does not have enough speed — the result will be a reduction of the orbit radius that generate a downward spiral toward the Earth; in simple words: it falls back to Earth.

There could be several causes for this:

Atmospheric Drag: Even in low Earth orbit, there are still thin traces of the atmosphere. These tiny air molecules create drag, which gradually slows down satellites over time. The lower the orbit, the denser the atmosphere. Satellites in very low orbits (below ~300 km) may only last a few days or weeks without propulsion. Without it, the drag will reduce the speed causing the satellite fall. Space stations, for instance, often fire thrusters occasionally to maintain altitude.

Launch Errors: during launch or deployment of satellites, there could be some errors due to engine malfunction, miscalculation, or staging error. This means that the satellite may never reach a stable orbit and quickly fall back.

Gravitational Perturbations: Other forces, such as the Moon’s gravity, Earth’s uneven mass distribution, or solar radiation pressure, can nudge a satellite and change its velocity slightly — though these effects are more significant over longer periods or in higher orbits.

To summarize, for low Earth orbits the most common problem is the drag, the others are negligible. Considering human knowledge, launch errors in terms of satellite deployment and proper speed are rare; there could be problems with the launchers but this will result in a mission abort. The gravitational perturbations are applicable, but are significant to higher orbits subjected to influence of other celestial bodies (e.g. Moon and Sun).

On the contrary, what is the satellite does provide much more speed than what is required to perform a circular orbit? There are infinite affordable orbits that we are going to deeply investigate in future articles. For the moment, it is useful to understand that a satellite with higher velocity can increase the radios of its original orbit or can either escape Earth’s gravity. This is what happens for all the deep space missions in which satellites are able to escape the gravitational field generated by the Earth to fly towards different planets in the Solar System.

Key Takeaways

I think we provides a lot of details on orbits, let’s summarize the key takeaways:

• Satellites stay in orbit by balancing gravitational pull with forward speed.
• The required speed depends on altitude; higher orbits need less speed.
• Orbital mechanics follow simple physical laws, but in practice, precise control is key.
• Drag and other forces can perturb satellite orbits to make them fall to the Earth.

We explained in this article the basics of the orbital mechanics, in our website you are able to find additional information on why planets keep spinning; maybe a little bit too advance for the moment, anyway in the future you will be able to follow it.

Want to learn more about orbital mechanics? Check our “Offering” and subscribe to our newsletter for upcoming deep dives!