The Gravitational Constant: The Magic that Rules Universe

Introduction

From the falling of an apple to the orbits of distant galaxies, the gravitational constant, expressed as G, is the invisible force binding everything in the universe. Though often overshadowed by more glamorous space concepts like black holes or rockets, G is fundamental to understanding celestial mechanics, orbital dynamics, and the very architecture of the cosmos.

What is the Gravitational Constant?

The gravitational constant (G) is the proportionality factor in Newton’s law of universal gravitation, which states:

(1) $\begin{equation*} F = G \frac{m_1 m_2}{r^2} \end{equation*}$

Where:

F is the gravitational force between two masses;
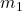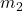$m_1$ , $m_2$ are the masses of the objects;
$r$ is the distance between their centers
G is the gravitational constant that is approximately $6.67430 \cdot 10^{-11} \, \frac{\text{N} \cdot \text{m}^{2}}{\text{kg}^{2}}$

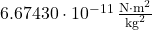
This constant allows us to quantify how much force of attraction exists between any two masses, anywhere in the universe.

History of Gravitational Constant

When Isaac Newton formulated his law of universal gravitation in 1687, he described how gravity acts between two masses. However, he never knew the value of G, neither able to calculate it. Newton’s law explained how gravity behaves, but did not quantify the actual strength of gravitational attraction in measurable units. In fact, in his Philosophiæ Naturalis Principia Mathematica he was able to postulates the inverse-square law of gravitation, and he was also able to identify a way to estimate the gravity’s strength by measuring the deflection of a pendulum in the vicinity of a large hill, but thought that the effect would be too small to be measurable.

It was not until more than a century later that scientists attempted to determine this elusive value.

The Cavendish Experiment (1798)

The first successful measurement of G came from British scientist Henry Cavendish, whose goal was not explicitly to find G but to “weigh the Earth.”

He used a torsion balance (see figure below) — a sensitive apparatus consisting of:

A lightweight horizontal bar suspended from a thin wire;
Small lead spheres attached to the ends of the bar (in the figure on the right, they are represented by the 2 red mass);
Two larger stationary spheres placed nearby.

When the large masses attracted the smaller ones via gravity, the bar would rotate, twisting the wire. Therefore, by measuring:

The angle of rotation;
The torsional resistance of the wire;
The known masses and distances;

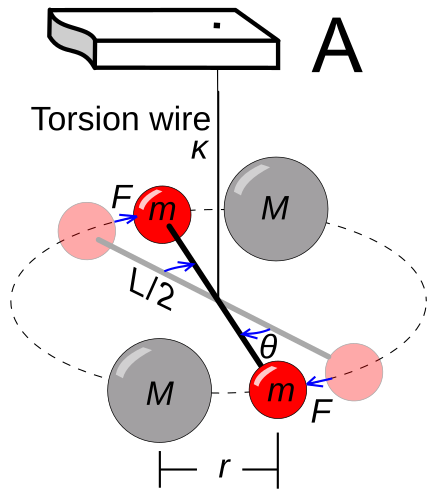
Cavendish was able to compute the tiny gravitational force between the masses. From this, he deduced the average density of the Earth, and later scientists derived the value of G from his data.

$G = \frac{F \cdot r^2}{m_1 m_2}$

The incredible fact is that this method was so precise for its time, that Cavendish’s value was within 1% of today’s accepted value!

Fun fact: Cavendish’s experiment was so delicate that it had to be performed in a sealed room, with observations made remotely using telescopes to avoid even the slightest air disturbance.

The Modern Value of G

The currently accepted value (as of CODATA 2018) is:

$G = 6.67430 \times 10^{-11} \, \text{m}^3 \cdot \text{kg}^{-1} \cdot \text{s}^{-2}$

But here’s the catch: G is one of the least precisely known physical constants. Its relative uncertainty is about 22 parts per million.

Why is Gravitational Constant So Hard to Measure?

Gravity is incredibly weak compared to other fundamental forces — for example, the electromagnetic force is 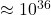$\approx 10^{36}$ times stronger.
Tiny gravitational effects are easily overwhelmed by:
- Vibrations
- Temperature variations
- Magnetic fields
- Air currents
Even modern experiments must be isolated in vacuum chambers and use ultra-sensitive and sophisticated equipment like laser interferometers and cryogenically cooled torsion balances. In fact, since Cavendish, many refined methods have emerged:
- Beam balances
- Atom interferometry: measuring how gravity affects ultra-cold atoms
- Torsion pendulums in vacuum
- Time-of-swing method: observing oscillation periods of a torsion pendulum

Despite advances, different labs still get slightly different values, a rare situation in fundamental physics. This inconsistency is often referred to as the “G problem.” In fact, G is one of the least precisely known constants in physics. Unlike the speed of light or Planck’s constant, which are measured to extreme precision, G’s value is still uncertain in the 5th decimal place. Experiments worldwide continue to refine it — a reminder of how challenging gravity is to isolate and study.

Mathematical Focus on the Gravitational Constant

Ok, we had a nice deep dive on the history of this constant and the methods to evaluate it. But let’s focus more on math.

Units of G

Considering the equation (1), it is possible to derive the units of G:

$\begin{equation*} [G] = \frac{[F] \cdot [r]^{2}}{[m_1] \cdot [m_2]} \end{equation*}$

Since $1 N = 1 kg \cdot m/s^2$ , we obtain the following unit for G:

$\begin{equation*} [G] = \frac{\text{kg} \cdot \text{m/s}^2 \cdot \text{m}^2}{\text{kg}^2} = \frac{\text{m}^3}{\text{kg} \cdot \text{s}^2} \end{equation*}$

Dimensional Analysis

Now that we found the units for G, it is possible to confirm the dimensional consistency of Newton’s law, starting again from equation (1).

For the ones that are not familiar with this method, the Dimensional analysis is a method used in physics and engineering to check the consistency of equations and to understand the relationships between physical quantities.

Every physical quantity has a dimension — such as length [L], mass [M], time [T], etc. In this specific case, we are focusing on the following dimensions:

Force $F: [M L T^{-2}]$
Mass $m: [M]$
Distance $r: [L]$

Substituting dimensions:

$\begin{equation*} [G] = \frac{[F] \cdot [r]^2}{[M]^2} = \frac{[M L T^{-2}] \cdot L^2}{M^2} = \frac{M L^3 T^{-2}}{M^2} = L^3 M^{-1} T^{-2} \end{equation}$

We found a perfect match with earlier unit analysis: $G \sim \text{m}^3 \cdot \text{kg}^{-1} \cdot \text{s}^{-2}$

The Role of Gravitational Constant in Orbital Mechanics

In many orbital mechanics problem, instead of using G and M (mass of a central body) separately, a gravitational parameter is defined:

$\begin{equation*} \mu = G \cdot M \end{equation}$

Object	Mean Radius $(km)$	Mass $(kg)$	$\mu = G \cdot m_1 (km \cdot s^{-2} )$
Sun	696 000	$1.989 \cdot 10^{30}$	$1.3271 \cdot 10^{11}$
Mercury	2 440	$3.302 \cdot 10^{23}$	$2.2032 \cdot 10^{4}$
Venus	6 052	$4.869 \cdot 10^{24}$	$3.2486 \cdot 10^{5}$
Earth	6378.14	$5.972 \cdot 10^{24}$	$3.986 \cdot 10^{5}$
Moon	1 738	$7.348 \cdot 10^{22}$	$4.904 \cdot 10^{3}$
Mars	3 397.4	$6.419 \cdot 10^{23}$	$4.2828 \cdot 10^{4}$
Jupiter	71 490	$1.8982 \cdot 10^{27}$	$1.2669 \cdot 10^{8}$
Saturn	60 270	$5.6834 \cdot 10^{26}$	$3.7931 \cdot 10^{7}$
Uranus	25 362	$8.6810 \cdot 10^{25}$	$5.7939 \cdot 10^{6}$
Neptune	24 622	$1.0241 \cdot 10^{26}$	$6.8365 \cdot 10^{6}$

All values are approximate averages, useful for the calculations and estimations that we are going to perform. For high-precision applications, refer to official sources like NASA’s planetary fact sheets.

The reader shall take into account another thing, before using the μ parameter. Let’s suppose that an artificial satellite is orbiting around the Earth.

$m_{Earth} = 5.972 \cdot 10^{24} = m_1$
$m_{satellite} = 10 000 kg = m_2$

Considering that $m_1 >> m_2$ , it is possible to perform the following approximation:

$\begin{equation*} \mu = G (m_1 + m_2) = G \cdot m_1 \end{equation*}$

In some cases, it is not possible to perform this approximation. A case is the analysis of the Moon orbits around the Earth, in fact here we will have:

$\begin{equation*} \mu = G (m_{Earth} + m_{Moon}) = \num{403\ 500} \ {\frac{km^{3}}{s^2} }\end{equation*}$

Considering only Earth mass, we will obtain $\mu = \num{398\ 600} \ {\frac{km^{3}}{s^2}$ , which means an error of:

$\begin{equation*} \epsilon = \frac{\num{398\ 600}}{\num{403\ 500}} \approx 0.98 % \end{equation*}$

It may not seem a huge error, but take into into account that this small error will propagate through the orbit. And considering the duration of certain space missions it can generate a huge error in orbit estimation.

What makes the Gravitational Constant So Important for Aerospace and Orbital Mechanics?

In aerospace engineering and orbital mechanics, G is the starting point for:

Orbital velocity calculations
Determining escape velocities
Modeling spacecraft trajectories
Calculating gravitational assists (slingshot maneuvers)
Simulating interplanetary transfers

To provide an example, check our article How Do Satellites Stay in Orbit? In order to understand how the Gravitational Constant can be used.

The Universality of the Gravitational Constant

A very interesting thing is that— as far as we can measure—G is constant throughout space and time.

Experiments in laboratories on Earth
Satellite data and planetary orbits
Observations of binary stars and galaxies

All show that G does not vary — at least not in any measurable way. It is considered universal.

Some alternative theories of gravity (like those in cosmology or string theory) explore if G might vary very slightly over cosmic time or in extreme conditions, but so far, no deviation has been confirmed.

Gravitational Constant in Einstein’s Relativity

In Einstein’s general relativity, G still plays a crucial role — but now it appears in Einstein’s field equations linking matter/energy and the curvature of spacetime:

$\begin{equation*} G_{\mu\nu} + \Lambda g_{\mu\nu} = \frac{8 \pi G}{c^4} T_{\mu\nu} \end{equation*}$

Einstein’s field equation (EFE) in its most general form. It connects spacetime curvature (geometry) with matter and energy (physics). It is divided into the following terms:

Einstein Tensor ( 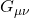$G_{\mu\nu}$ : Describes how spacetime is curved due to the presence of mass-energy. It is built from the Ricci curvature tensor and the metric tensor. Essentially explain How space-time bends.
Metric Tensor ( 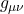$g_{\mu\nu}$ : Describes the shape and geometry of spacetime. It defines distances, angles, and time intervals between points in curved space.
Cosmological Constant ( 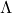$\Lambda$ : Originally introduced by Einstein to allow a static universe (later dropped, now used in dark energy models). Represents a uniform energy density filling space.
Stress-Energy Tensor ( 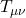$T_{\mu\nu}$ : Contains all forms of energy, momentum, pressure, and stress in spacetime. Represents “what’s inside” space: matter, radiation, etc.
Coupling Constant ( 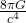$\frac{8\pi G}{c^4}$ : Tells how much spacetime is curved by a given amount of energy or mass. Ensures the correct units and scale.

“Mass and energy tell spacetime how to curve, and curved spacetime tells objects how to move.”

This equation replaces Newton’s law of gravitation in the relativistic regime (i.e., near massive objects, at high speeds, or in cosmology).

There are also some interesting real world implications:

Black holes: Predicted as regions where spacetime curvature becomes infinite.
Gravitational waves: Ripples in spacetime, predicted by EFE and detected in 2015.
Cosmology: The equation forms the basis of models of the expanding universe.
GPS systems: Require relativistic corrections due to the curvature of spacetime around Earth.

This elevates G from a simple force constant to a cosmic connector between mass and the geometry of the universe.

Key Takeaways of Gravitational Constant

The gravitational constant, might look like just a tiny number in equations, but it plays a massive role in our understanding of the universe. It sets the scale for gravity — the force that binds the cosmos together, from falling objects on Earth to the orbits of moons, planets, and galaxies.

Despite being one of the weakest forces compared to electromagnetism or nuclear forces, gravity dominates on large scales, and G is the key to unlocking its behavior.

Whether you’re calculating how a satellite orbits Earth or diving into Einstein’s theory of general relativity, the constant G is always there — connecting mass, space, time, and curvature.

In the present articles we explore so many topics, I would like just to sum up the key concepts:

What is G?
It defines the strength of the gravitational force between two masses.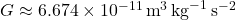 $G \approx 6.674 \times 10^{-11} \, \text{m}^3 \, \text{kg}^{-1} \, \text{s}^{-2}$

It’s universal:
So far, experiments confirm that G is the same everywhere in the universe, and at all times.

It is essential in orbital mechanics:
G is used in calculating gravitational forces, planetary motion, and spacecraft trajectories. (see also How Do Satellites Stay in Orbit?)

It plays a key role in general relativity:
It appears in Einstein’s field equations, where it links mass-energy to the curvature of spacetime.

Difficult to measure precisely:
Despite being fundamental, G is one of the least precisely known constants due to the extreme weakness of gravity.

FAQ on Gravitational Constant

Q1: What is the gravitational constant?
The gravitational constant (G) is a fundamental physical constant that appears in Newton’s law of universal gravitation. It quantifies the strength of the gravitational force between two masses.

Q2: What is the value of G?
The accepted value is: $G = 6.67430 \times 10^{-11} \, \text{m}^3 \text{kg}^{-1} \text{s}^{-2}$

(This is based on CODATA 2018 recommendations.)

Q3: Who discovered the gravitational constant?
G was first measured by Henry Cavendish in 1798 using a torsion balance experiment. He didn’t directly call it “G,” but his work allowed later scientists to calculate it.

Q4: Why is G important?

It determines the strength of gravity in Newton’s law: $F = G \frac{m_1 m_2}{r^2}$
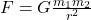
It allows calculation of planetary orbits, satellite motion, and cosmic phenomena.
It’s crucial in Einstein’s general relativity, appearing in Einstein’s field equations.

Q5: Why is G so hard to measure accurately?
Gravity is extremely weak compared to other fundamental forces. Even tiny vibrations, temperature changes, or nearby masses can affect measurements, leading to slight discrepancies in experimental results.

Q6: Does G change over time or in space?
Current evidence suggests that G is constant throughout the observable universe and over time. However, some alternative physics theories predict tiny variations, but none have been confirmed experimentally.

Q7: What are the units of G? m3kg−1s−2\text{m}^3 \text{kg}^{-1} \text{s}^{-2}m3kg−1s−2

These units come from rearranging Newton’s law of gravitation.

Q8: Is G the same as g?
❌ No. The two parameters are different:

G = Universal gravitational constant (fundamental constant).
g ≈ 9.81 m/s² = Gravitational acceleration at Earth’s surface.

In practice, g is the local effect (Earth’s pull), and G is the universal constant that makes g calculable.

Q9: How precise is our knowledge of G compared to other constants?
G is one of the least precisely known fundamental constants — its relative uncertainty is about 20 parts per million, much worse than constants like the speed of light or Planck’s constant.

Q10: What experiments are used to measure G?

Cavendish torsion balance (classic method).
Atom interferometry (modern quantum methods).
Pendulum-based methods and beam balances.

Q11: Is G a strong force?
❌ No, gravity is the weakest of the four fundamental forces.

The gravitational attraction between two protons is 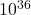$10^{36}$ times weaker than their electric repulsion.
This is why measuring G is so difficult — gravity’s pull is faint compared to electromagnetic, strong nuclear, and weak nuclear forces.

The Gravitational Constant: The Magic that Rules Universe

Table of Contents

Introduction

What is the Gravitational Constant?