Table of Contents
Introduction on Geosynchronous Orbit
A geosynchronous orbit is a special type of orbit where a satellite revolves around Earth at the same rate that the planet rotates on its axis. This synchronization means the satellite appears to return to the same position in the sky at the same time each day, making geosynchronous orbits invaluable for communications, weather monitoring, and surveillance.
Unlike low-Earth orbits or medium-Earth orbits, a geosynchronous orbit requires very precise positioning and velocity calculations. To achieve this, engineers rely on the geosynchronous orbit equation and related orbital mechanics principles to ensure satellites maintain the correct altitude and period.
In this article, we are going to investigate the Geosynchronous Orbit Equation, we will discover how to compute the Geosynchronous Orbit Radius and altitude, we will compare it with the Geostationary Orbit Equation and we will identify and explain concrete examples and simulation.
Geosynchronous Orbit Equation
The geosynchronous orbit equation is derived from balancing gravitational force and centripetal force acting on a satellite. Earth’s gravity provides the necessary centripetal force to keep the satellite in orbit, and this balance can be expressed mathematically:
![]()
Where:
- T = orbital period (for geosynchronous orbit, this is 86,164 seconds, or about 23 hours 56 minutes),
- r = orbital radius from Earth’s center,
- G = universal gravitational constant (
![Rendered by QuickLaTeX.com 6.674 \cdot 10^{-11} \ \text{N·m}^2/\text{kg}^2),</li> <!-- /wp:list-item --> <!-- wp:list-item --> <li>M = mass of the Earth ([latex] 5.972 \times 10^{24} \, \text{kg}](https://theengineeringhub.it/wp-content/ql-cache/quicklatex.com-0d0457ff74dc2550c4edd5e6a105d8db_l3.png) ).
).
This formula is critical in determining the geosynchronous orbit radius, the distance from Earth’s center where a satellite must orbit to remain synchronized with the planet’s rotation.
Calculating the Geosynchronous Orbit Radius
Using the above geosynchronous orbit formula, scientists and engineers can solve for r (the geosynchronous orbit radius):
![]()
Plugging in the known values gives:
![]()
Since Earth’s mean radius is about 6,378 km, the satellite’s altitude or in other words the Geosynchronous Orbit Altitude above the surface is:
![]()
This altitude is a defining characteristic of all geosynchronous satellites.
Geosynchronous vs. Geostationary Orbits
Though often used interchangeably, geosynchronous orbit and geostationary orbit are not identical. A geosynchronous satellite may have an inclined or elliptical orbit, meaning it traces a figure-eight (analemma) pattern in the sky.
What is important to highlight is that geostationary orbits are particular geosynchronous orbit. A geosynchronous orbit (GEO) is a prograde, low inclination orbit about Earth having a period of 23 hours 56 minutes 4 seconds (sidereal day). The spacecraft returns to the same point in the sky at the same time each day. Instead, geostationary orbits, is a specific type of geosynchronous orbit that is perfectly circular and directly above Earth’s equator. From the ground, a geostationary satellite appears to remain completely stationary at a fixed point in the sky—ideal for telecommunications and broadcasting.
Geosynchronous Orbits has less constraints in terms of eccentricity and inclination. Geostationary orbit (also called GEO) is ideal for satellites that need to stay fixed above a specific location, such as telecommunication satellites, allowing antennas on Earth to stay in a constant position, always pointing at the satellite.
Below, we are providing a brief table to show the differences between geosynchronous and geostationary orbits.
| Feature | Geosynchronous | Geostationary |
|---|---|---|
| Orbital period | ≈ 23h 56m (sidereal day) | ≈ 23h 56m (sidereal day) |
| Orbit shape | Can be elliptical or circular | Must be circular |
| Inclination | Any inclination (0° to ~63°) | 0° (equatorial) |
| Ground track | Forms a figure-8 or loop in the sky | Appears fixed above the equator |
| Motion | Satellite appears to move relative to Earth | Satellite appears stationary to an observer |
| Use cases | Reconnaissance, scientific, some comsats | TV, weather satellites, communications (e.g. TV) |
Simulating a Geosynchronous Orbit
Let’s simulate a Geosynchronous Earth Orbit! First, let’s focus on the appearance of the orbit, even if it is not so meaningful. Below, you will find a brief simulation that shows an orbit of satellite in the following condition:
Geosynchronous Orbit with Low Inclination, Zero eccentricity
- r = 41,164 km
- eccentricity = 0
- orbit inclination = 10°
Not so useful, right? But, what is really interesting of Geosynchronous Orbit is the ground track.
Ground track: The ground track of a satellite is the path on Earth’s surface directly beneath the satellite as it orbits the planet. In other words, it is the projection of the satellite’s orbit onto Earth.
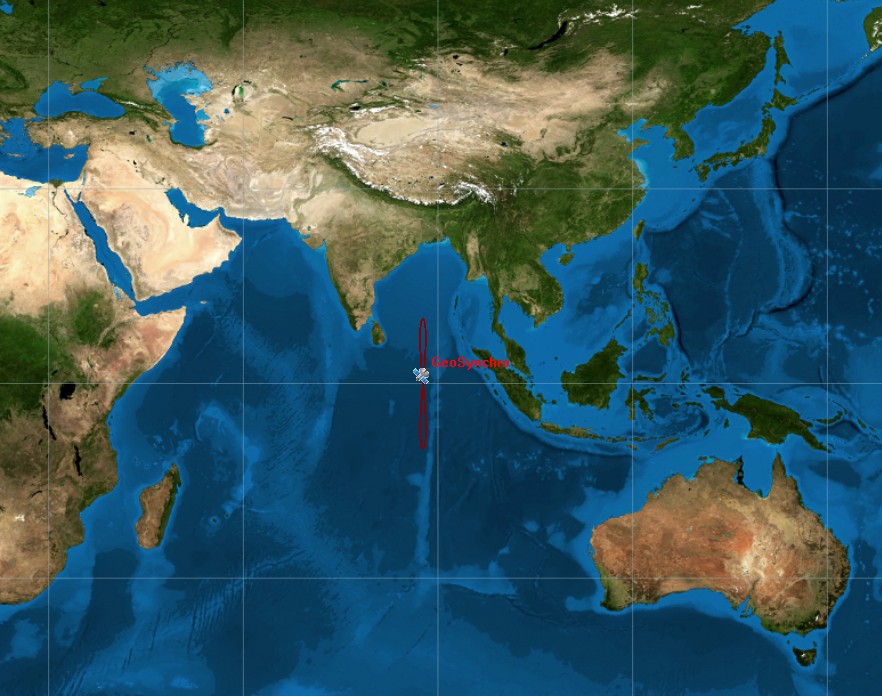
In the picture it is possible to see a geosynchronous satellite with a low inclined orbit (ref. to above mentioned data). The interesting fact is that the ground track appears as an eight figure also called analemma. In this case we are talking about a symmetric analemma, since the eight figure is perfect: the 2 lobes are identical and satellite passes the same amount of time in the northern and southern parts.
Geosynchronous Orbit with Low Inclination, Low eccentricity
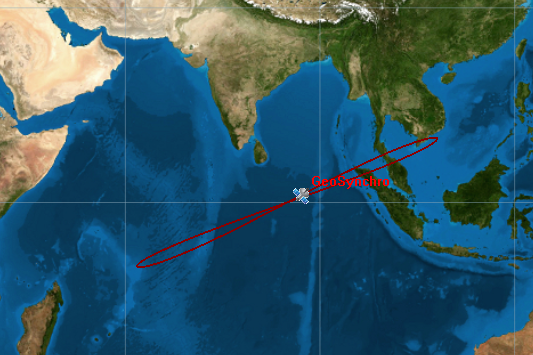
Let’s mix some data update the results:
- r = 41,164 km
- eccentricity = 0.2
- orbit inclination = 10°
It is possible to see that the result is unbalanced in terms of shape.
What is important to understand is the fact that due to change in eccentricity, the eight, drawn on Earth by the satellite, is rotating clockwise.
Again, it is possible to see that the more eccentricity we have the more stretch the orbit is. In this case, we applied the following data:
- r = 41,164 km
- eccentricity = 0.3
- orbit inclination = 10°
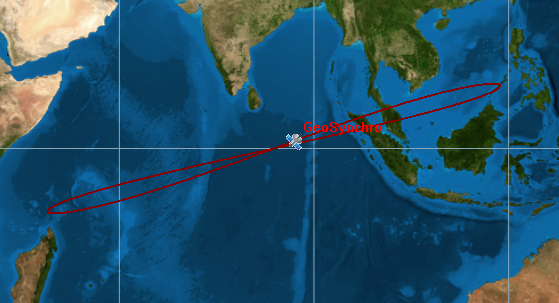
Geosynchronous Orbit with Low Inclination, High eccentricity
In this case, again the orbit became larger, since the eccentricity increased. One important result is that even if we are modifying the eccentricity, the orbit is always symmetric, this is valid if the Argument of Periapsis ![]() is equal to zero.
is equal to zero.
Below the data used:
- r = 41,164 km
- eccentricity = 0.7
- orbit inclination = 10°
Geosynchronous Orbit with High Inclination, Low eccentricity
Let’s focus on a different case, eccentricity equal to zero and high inclination. In this case, orbit is more round and obviously it is possible to see that the ground track reaches a higher latitude. Below, the data shown in the picture on the right:
- r = 41,164 km
- eccentricity = 0
- orbit inclination = 50°
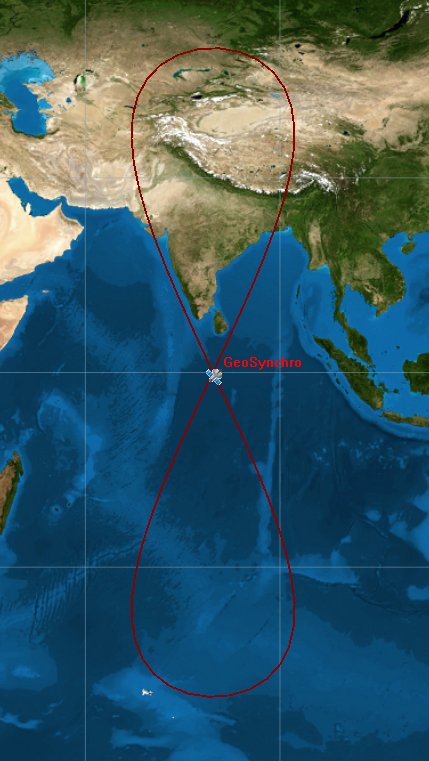
Geosynchronous Orbit with High Inclination, High eccentricity
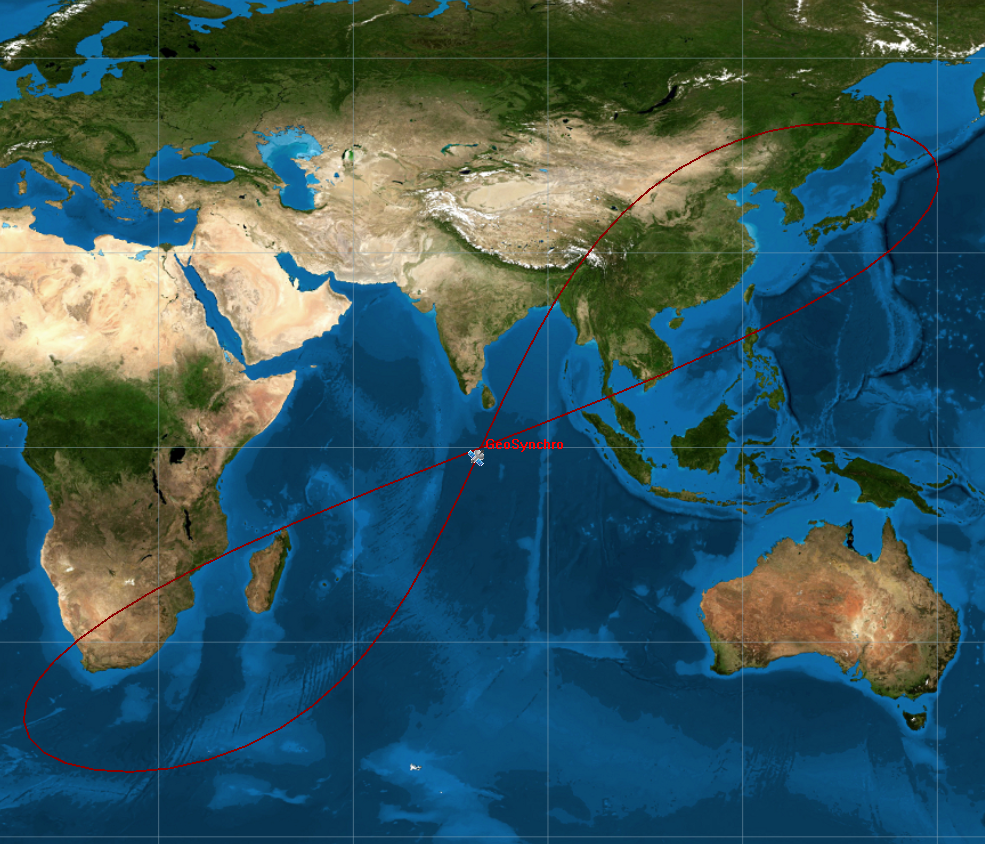
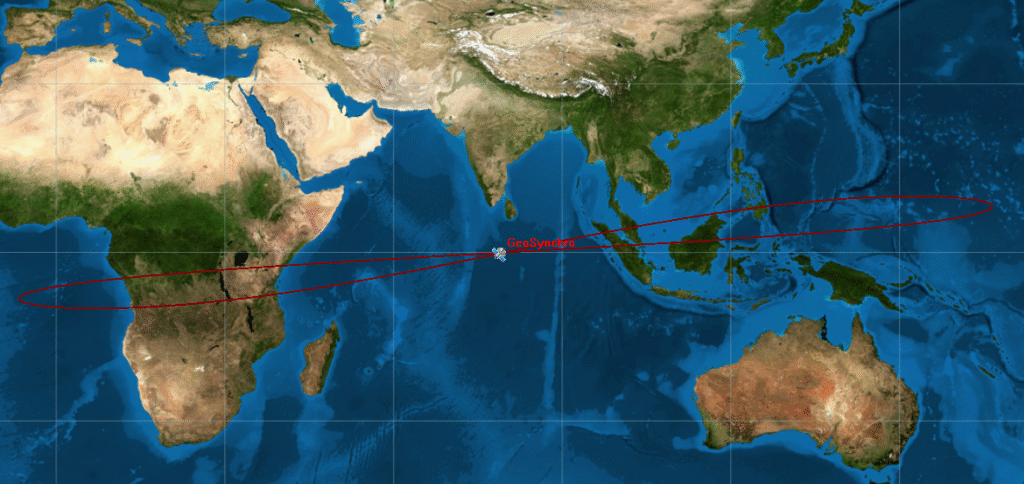
To conclude, we can guess also the case with high eccentricity and inclination. In this case, we see the clockwise rotation of the orbit, still symmetrical, but with a higher latitude point compared to the low orbit inclination seen before. The image on the left is made using the following data:
- r = 41,164 km
- eccentricity = 0.5
- orbit inclination = 50°
Launching a Geosynchronous Satellite
Placing a satellite into geosynchronous orbit (GSO) is among the most demanding tasks in spaceflight, requiring precise planning and significant energy. The goal is to position the satellite at an altitude of 35,786 km (geosynchronous orbit altitude) above Earth’s surface, where it completes one revolution every 24 hours, matching Earth’s rotation. This requires meticulous planning, multiple orbital maneuvers, and often months of preparation before the satellite becomes operational.
Launch Vehicle Selection
Because geosynchronous orbits demand high energy (a delta-v of roughly 10 km/s from Earth’s surface), powerful launch vehicles such as Ariane 5/6, Falcon Heavy, or Atlas V are typically used (if you are looking for a brief history of launch vehicles read our article on the evolution of rocket propulsion). These rockets can deliver payloads into a Geosynchronous Transfer Orbit (GTO) — an elliptical orbit that serves as the first step toward the final geosynchronous position.
Reaching Geosynchronous Transfer Orbit (GTO)
- The satellite is first launched into Low Earth Orbit (LEO).
- From there, the rocket’s upper stage performs a perigee burn, raising the apogee to geosynchronous orbit altitude while keeping the perigee low.
- The resulting orbit is highly elliptical, with an apogee near 35,786 km.
Transfer to Geosynchronous Orbit
Once at apogee, the satellite fires its apogee kick motor (AKM) or electric propulsion system. This maneuver will apply in order to:
- Circularizes the orbit at 35,786 km, turning the GTO into a true geosynchronous orbit.
- Adjusts inclination to near-zero if a geostationary position is desired (this requires extra fuel if launched from higher latitudes).
Orbital Slot Assignment and Station-Keeping
- Satellites in GSO are placed into specific orbital slots (longitudes) assigned by the International Telecommunication Union (ITU).
- Once operational, the satellite performs station-keeping maneuvers to counteract gravitational perturbations from the Moon, Sun, and Earth’s equatorial bulge, as well as solar radiation pressure.
Operational Handover
After weeks of testing and calibration, the satellite is declared operational and begins its mission — whether for telecommunications, weather observation, or military monitoring.
Applications of Geosynchronous Orbits
As mentioned briefly above, satellites in geosynchronous orbit serve critical global functions:
- Telecommunications: Providing continuous coverage for television, internet, and phone networks.
- Weather forecasting: Satellites like GOES (Geostationary Operational Environmental Satellites) monitor storms and climate patterns.
- Military and surveillance: Governments use geosynchronous satellites for strategic monitoring and secure communications.
Tundra, Super Tundra, and Molniya Orbits
When most people think of geosynchronous satellites, they picture geostationary orbit (GEO) — the famous “ring” of satellites 35,786 km above the equator, appearing fixed in the sky. GEO is perfect for TV, weather, and communications, but it has one major flaw: it doesn’t serve high-latitude regions well.
For places like Russia, Canada, and the Arctic, satellites sitting low on the horizon provide poor coverage. Engineers came up with clever alternatives: tundra orbits, super tundra orbits, and Molniya orbits — all designed to “park” satellites over northern regions for long periods of time.
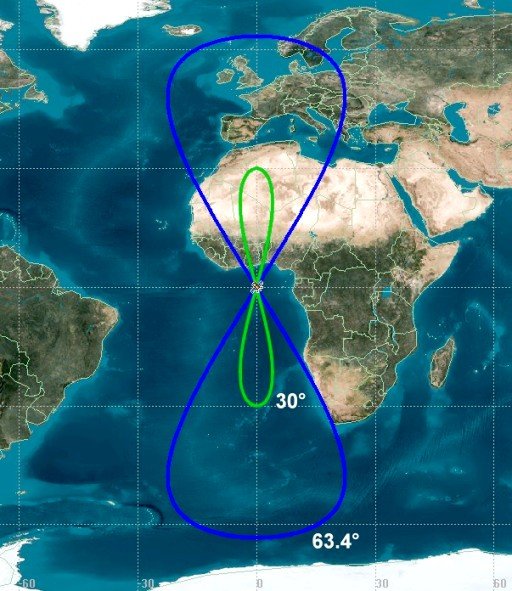
Tundra Orbit
A tundra orbit is a highly elliptical geosynchronous orbit with:
- 24-hour period (like GEO)
- Inclination ~63.4° (a “critical” angle that stabilizes the orbit against Earth’s gravity bulge)
- Eccentricity ~0.2 (elongated shape)
- Argument of Periapsis = -90°
How it works
- The satellite slows down dramatically near apogee (the farthest point)
- It “lingers” for up to 8–12 hours over the northern hemisphere
- Two or three satellites can provide near-constant coverage
Real examples
- Sirius Satellite Radio used three tundra satellites to provide radio across North America.
- Russia’s Meridian satellites use tundra orbits for Arctic communications.
Super Tundra Orbit
A super tundra orbit is essentially a scaled-up version of the tundra orbit:
- Still geosynchronous (24-hour period)
- Even higher apogee (beyond typical tundra ranges)
- Often used for space debris monitoring, experimental satellites, and long-term surveillance
Why use it?
- Provides even longer dwell time over key areas
- Can cover more remote regions with fewer satellites
- Rarely used in commercial systems, but studied for deep-space gateway communications and strategic monitoring
Potential use cases
- Proposed for early-warning missile detection and future Arctic internet constellations
- Sometimes used in simulation or academic studies for “extended tundra” coverage scenarios
Molniya Orbit
The Molniya orbit predates tundra — developed by the Soviet Union in the 1960s.
- 12-hour period (not geosynchronous — completes 2 orbits per day)
- Inclination ~63.4° (same “critical” angle as tundra)
- Very high eccentricity (~0.7)
How it works
- Satellite spends ~8 hours near apogee each orbit
- Provides extended coverage of northern latitudes
- Requires 3 or more satellites for continuous service
Real examples
- Soviet Molniya satellites revolutionized TV & communications for Siberia and the Arctic.
- Used for early-warning (Oko program), civilian telecom, and even intelligence gathering.
Brief comparison between GEO, Tundra, Super Tundra and Molniya
| Orbit Type | Period | Inclination | Eccentricity | Coverage Goal |
|---|---|---|---|---|
| Geostationary (GEO) | 24 hrs | 0° | 0 (circular) | Equator-focused |
| Tundra | 24 hrs | 63.4° | ~0.2 | Lingering over high latitudes |
| Super Tundra | 24 hrs | 63.4°+ | ~0.2+ | Longer dwell time, experimental/strategic |
| Molniya | 12 hrs | 63.4° | ~0.7 | Repeated long passes over high latitudes |
Challenges in Maintaining Orbit
On paper, a geosynchronous orbit sounds simple: put a satellite 35,786 km above Earth, match Earth’s rotation, and it “hangs” over one spot!
But in practice, it’s not a set-and-forget orbit — it takes regular corrections. Here’s why:
Earth is not a perfect sphere
- Earth is slightly flattened at the poles and bulged at the equator — an effect called the oblateness (the J2 term in orbital mechanics). We will discover it in a dedicated article!
- This uneven gravity field causes a geosynchronous satellite’s inclination and longitude to drift over time.
- Without station-keeping, the satellite would slowly “wander” north–south (forming a figure‑8 pattern) and east–west across the sky.
Gravitational pulls from the Moon and Sun
- The Moon and Sun tug on geosynchronous satellites.
- These tugs change the satellite’s inclination over time, slowly “tilting” the orbit unless corrected.
Solar radiation pressure
- Sunlight itself exerts a tiny but constant pressure on satellites.
- Over months and years, this force nudges the orbit, altering its eccentricity (making it less circular) and causing drift.
Station‑keeping “boxes”
- Each operator is assigned a geostationary slot (e.g., “154° West longitude”).
- International regulations (via the ITU) require satellites to stay within a small “box” (often ±0.05°).
- Without frequent adjustments (fuel burns), the satellite would drift out of this box and interfere with neighbors.
Fuel limitations
- To correct all these effects, geosynchronous satellites need station‑keeping maneuvers using onboard fuel.
- Fuel eventually runs out — at which point the satellite is moved to a “graveyard orbit” a few hundred kilometers higher.
Bottom line
Maintaining a geosynchronous orbit is hard because:
- The orbit is constantly perturbed by Earth’s shape, the Moon, the Sun, and solar pressure.
- Satellites must stay in a very tight tolerance zone for decades.
- Every correction uses finite fuel, which ultimately limits the satellite’s life.
Conclusion
The concept of a geosynchronous orbit underpins modern communication, navigation, and observation systems. We highlight the principal characteristic of this orbit: to return to the same spot every day at a certain time. By applying the geosynchronous orbit equation, engineers determine the exact geosynchronous orbit radius necessary for satellites to stay synchronized with Earth’s rotation. This precise balance of physics and technology allows us to enjoy services ranging from live global broadcasts to real-time weather data—reminders of how orbital mechanics shape everyday life.
In this article we analyzed the characteristics of Geosynchronous orbits and we discover some examples that will be deeply analyzed in the next articles. In addition, we explained the maneuvers to reach the geosynchronous orbit altitude and we provide some details on why is not so easy to manage these kind of orbits.
❓FAQ: Geosynchronous Orbits
Q1: What’s the difference between geosynchronous and geostationary?
- Geosynchronous means the satellite’s orbital period is exactly 24 hours, so it returns to the same spot in the sky every day.
- Geostationary is a special type of geosynchronous orbit that is perfectly circular and sits directly above the equator (0° inclination), so the satellite appears completely fixed over one longitude.
Q2: Why are geosynchronous orbits 35,786 km high?
That’s the altitude where the satellite’s orbital period naturally matches Earth’s rotation (a sidereal day). If it’s lower, it would orbit too fast; higher, it would orbit too slow.
Q3: Why is it so hard to keep satellites in place in these orbits?
- Earth isn’t a perfect sphere (its bulge nudges the orbit).
- The Moon and Sun pull on the satellite.
- Solar radiation slowly pushes on it like a “light wind.”
- Without constant corrections (station‑keeping maneuvers), it would drift away from its assigned slot.
Q4: What happens when a geosynchronous satellite runs out of fuel?
When fuel is gone, operators boost it a few hundred kilometers into a “graveyard orbit.” This keeps the busy geostationary belt clear of dead satellites and avoids collisions.
Q5: Why don’t geostationary satellites work well for polar regions?
From high latitudes (like Canada or Russia), a GEO satellite sits very low on the horizon, which:
- Weakens the signal
- Causes issues with mountains, buildings, or terrain blocking the line of sight
That’s why countries at high latitudes use Molniya and Tundra orbits instead.
Q6: How long can a geosynchronous satellite last?
Typically 10–15 years. The main life‑limiting factor is station‑keeping fuel — once that’s gone, the satellite cannot hold position.


Pingback: A Comprehensive Guide on Earth Orbit: How Satellites Move in Space